4-1 (1 weg, 4 weg) Crawford

Von Kit Woolsey, 1998 veröffentlicht hier: bkgm.com 

Freie Übersetzung: Miriam Wieck und Torsten Lux 
 
Kommentare: Torsten Lux 

Wir haben es scheinbar mit einer ähnlichen Situation wie beim 4-3 Crawford Spielstand zu tun. Gammons haben für den zurückliegenden Spieler einen extra Wert, da ein Gammon-Sieg den Spielstand auf 3:4 erhöhen würde. Das Crawford-Spiel wäre dann abgehakt, so dass der zurückliegende Spieler wieder doppeln kann. Abgesehen vom leichten Vorteil, der dem führenden Spieler aus seiner Möglichkeit zum Free Drop erwächst, ist die Situation ausgeglichen. 

Wie sich herausstellt, gibt es jedoch einen entscheidenden Unterschied: Wenn der zurückliegende Spieler einfach gewinnt (also 2-4), muss er nicht unbedingt zwei weitere Partien gewinnen, um als Sieger aus dem Match hervorzugehen. Er könnte auch ein Gammon gewinnen.  

Um die ungefähren Chancen des zurückliegenden Spielers nach dem Spielstand 4:2 Post-Crawford zu ermitteln, nehmen wir an, dass er die folgende Partie in 50 % der Fälle gewinnt, und dass 24 % seiner Siege Gammons sind (was 12 % der gesamten Spiele entspricht).  

• Der führende Spieler gewinnt 50 % (100 % Match Equity für den führenden Spieler) 
• Der zurückliegende Spieler gewinnt einfach zu 38 % (50 % Match Equity für den führenden Spieler) 
• Der zurückliegende Spieler gewinnt Gammon (0 % Match Equity für den führenden Spieler) 

Zusammengerechnet ergibt sich für den führenden Spieler eine Equity von 50 x 100 plus 38 x 12 = 69 %.  

Jetzt können wir die Chancen des zurückliegenden Spielers berechnen, wenn er ein riskantes Spiel macht, um ein Gammon beim Stand von 1:4 zu gewinnen: 

• Der führende Spieler gewinnt: Die Equity des zurückliegenden Spielers beträgt 0 %. 
• Der zurückliegende Spieler gewinnt: Die Equity des zurückliegenden Spielers beträgt 31 %. 
• Der zurückliegende Spieler gewinnt Gammon: Die Equity des zurückliegenden Spielers beträgt 49 % (der führende Spieler erhält 1 % für den Free Drop). 

Das bedeutet, dass der zurückliegende Spieler, falls er eine riskante Spielweise wählt, bei der er den Gewinn der Partie aufs Spiel setzt, um seine Gammon-Chancen zu erhöhen, 31 % Match Equity riskiert, um sie um18 % zu steigern. Diese Einsätze sind weit entfernt von den ausgeglichenen Einsätzen, die der zurückliegende Spieler bei einem Spielstand von 4:3 erhält; tatsächlich liegen sie ziemlich nahe an den normalen Quoten von 2:1. Obwohl Gammons also für den zurückliegenden Spieler von Bedeutung sind, sind sie nicht so wichtig, wie sie es bei einem ausgeglichenen Spielstand wären, bei dem es für beide Spieler um die gleichen Einsätze geht.  

Ein weiterer wichtiger Aspekt bei diesem Spielstand ist die Unwichtigkeit von Backgammons. Wie wir gesehen haben, gibt es kaum einen Unterschied zwischen 4-4 und 4-3 Post Crawford. Folglich kann der führende Spieler das Backgammon-Risiko ignorieren, wenn eine Chance besteht, das Gammon zu retten oder sogar das Spiel zu gewinnen.

Ein extremes Beispiel:

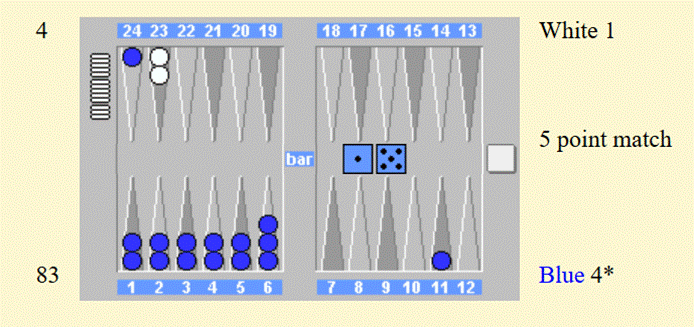
Unter normalen Umständen wäre jeder andere Zug außer 24/18 töricht. Die Gefahr, ein Backgammon zu verlieren, überwiegt bei weitem die Vorteile, die sich aus dem mit der Hoffnung auf einen möglichen letzten Schuss verknüpften Stehenbleiben ergeben. 
Bei diesem Spielstand jedoch sind Backgammons praktisch bedeutungslos – es ist korrekt, wenn Blau 11/5 spielt. Wenn Weiß eine 1 würfelt und Blau den Schuss trifft, kommt er definitiv aus dem Gammon heraus, und an einem sehr guten Tag könnte er das Spiel sogar gewinnen.  

Der Gewinn ist größer als die winzigen Kosten für den Backgammon-Verlust im Vergleich zum Gammon-Verlust, da alles, was Blau durch die Rettung des Backgammons gewinnen würde, aus dem Free Drop in der nächsten Partie besteht.  

Auch wenn diese Spielweise Blau viel öfter einen Backgammon-Verlust bescheren wird, als dass es den Gammon-Verlust abwendet oder das Spiel gewinnt, ist sie bei diesem Spielstand richtig.